Resumen

El problema de la p-mediana es un modelo de optimización matemática que consiste en ubicar p localizaciones de una red de manera que la distancia ponderada entre los puntos de demanda y la instalación abierta más cercana sea mínima. Este proyecto explica su fundamento teórico y expone una aplicación que propone optimizar la distribución de los consultorios de Atención Primaria de Castilla y León.

Introducción

En los últimos años, debido al descenso de la población de Castilla y León y, en particular, de sus zonas rurales, ha surgido un problema de despoblación. Además, el número de médicos en atención primaria se ha visto reducido: en 2017 había 2.900 médicos de familia mientras que en 2021 había 2.465, es decir, 435 profesionales menos en 4 años.[14]

Según los datos del Ministerio de Sanidad, en 2020 (último año del que hay datos publicados) Castilla y León fue la comunidad autónoma que más dinero invirtió en sanidad pública por habitante protegido y la segunda que más porcentaje destinó de este dinero a la Atención Primaria, solo por detrás de Andalucía. Es también la comunidad que tiene una mayor tasa de profesionales de Atención Primaria por cada 1.000 habitantes (1,12 prof./1.000 hab), siendo la única que supera el profesional por cada millar de habitantes. En Atención Especializada es la séptima comunidad con mayor tasa de personal médico por millar de habitantes. A pesar de estos datos, en 2019 tenía la octava mejor valoración de la atención médica entre las comunidades autónomas y quedan numerosas plazas de trabajo sin cubrir.[12][2][1]

Todos estos datos nos inducen a pensar que el sistema sanitario de Castilla y León y, en particular los recursos de Atención Primaria, no están optimizados. Es por esto que vamos a proponer un modelo de distribución de los consultorios y centros de atención primaria de acuerdo a las características particulares de la comunidad.

Conviene destacar que los municipios de Castilla y León se encuentran muy dispersos por todo el territorio, con las capitales de provincia como principales núcleos de población y numerosas poblaciones, con pocos habitantes en su mayoría, en el resto del territorio. Un acceso óptimo a los recursos sanitarios en todo el territorio favorecerá la recuperación de la ''España Vaciada'' y solventará el problema de personal sanitario que hay en la comunidad.

El objetivo de este trabajo es proponer una redistribución de los consultorios de atención primaria teniendo en cuenta la distribución de la población en el territorio, las distancias entre los núcleos de población y la actual disposición de los consultorios, mediante un modelo matemático. Además propondremos posibles mejoras de este modelo considerando el tiempo de traslado entre poblaciones (una determinada distancia por carretera de montaña se tarda más en recorrer que por autovía), la frecuentación de los consultorios actuales, la edad de los pacientes (zonas con más ancianos o bebés requerirán mayor atención), la presión asistencial, cercanía a establecimientos farmacéuticos y otros modelos matemáticos que podrían adaptarse a este problema.

Para realizar este estudio nos centraremos en el problema de la p-mediana: consideraremos la distribución actual de los consultorios como un grafo y buscaremos los nodos que minimizan el ''costo'' de establecer un determinado número de bases que serán los nuevos consultorios. El valor que queramos minimizar será el que consideremos el ''costo'' de la instalación.

En caso de que quisiéramos reducir el número de consultorios (caso en el que se centra este trabajo), los pacientes de los consultorios que ya no se utilizarían podrían ser tratados en los nuevos consultorios (colocados de forma óptima según el modelo) o atendidos mediante un vehículo medicalizado si así se considerara adecuado. Una reducción adecuada del número de consultorios facilitaría una mayor dotación de material y personal sanitario a los que se establecieran, por lo que la atención mejoraría.

Para este estudio utilizaremos los datos de consultorios, zonas básicas de salud, frecuentación, presión asistencial, población, tarjetas sanitarias, consultas y establecimientos sanitarios del portal de datos abiertos de la Junta de Castilla y León y del portal de datos abiertos de sanidad de Castilla y León. Los datos comparativos con otras comunidades autónomas han sido extraídos de la aplicación de indicadores claves del Sistema Nacional de Salud del Ministerio de Sanidad, Consumo y Bienestar Social.

Objetivos

Visibilizar la necesidad de una reforma en el sistema sanitario de Castilla y León.
Proponer un modelo matemático para mejorar la gestión de la atención primaria rural en Castilla y León.
Proponer una redistribución de los consultorios rurales para una mejor gestión de los recursos y una mejor atención a los pacientes.
Analizar posibles mejoras a dicho modelo y proponer otras alternativas.
Visibilizar la aplicación de las matemáticas para la resolución de problemas.

Fundamento teórico

En este apartado vamos a explicar las herramientas matemáticas en las que se basa el modelo que vamos a utilizar para la redistribución de los consultorios rurales.

Definiciones

Sea $X$ un conjunto no vacío y sea $f : X \to ℝ$ una función dada. Consideramos el problema de minimización:

\min f (x) sujeto a x \in X

(1)

La función $f$ se denomina función objetivo del problema (1) y el conjunto $X$ es el conjunto factible de (1). Si $X = ℝ^{n}$ el problema (1) es un problema de optimización sin restricciones. En otro caso tenemos un problema de optimización con restricciones.

También podemos considerar el problema de maximización:

\max f (x) sujeto a x \in X

(2)

Definición 4.1. Un vector $x \in ℝ^{n}$ es factible para (1) si $x \in X$ .

Definición 4.2. Un vector factible $x^{∗}$ para (1) es un mínimo global de (1) si $f (x^{∗}) \leq f (x) \forall x \in X$

Definición 4.3. Un vector factible $x^{∗}$ para (1) es un mínimo local de (1) si existe un $𝜖 > 0$ tal que $f (x^{∗}) \leq f (x) \forall x \in X \cap B_{𝜖} (x^{∗})$ , donde $B_{𝜖} (x^{∗}) : = {x \in ℝ^{n} | ∥ x - x^{x *} ∥ < 𝜖}$ denota la bola euclídea de radio $𝜖 > 0$ alrededor del punto $x^{∗}$

Definición 4.4. Un vector factible $x^{∗}$ para (1) es un mínimo global estricto de (1) si $f (x^{∗}) \leq f (x) \forall x \in X$ con $x \neq x^{∗}$

Definición 4.5. Un vector factible $x^{∗}$ para (1) es un mínimo local estricto de (1) si existe un $𝜖 > 0$ tal que $f (x^{∗}) \leq f (x) \forall x \in X \cap B_{𝜖} (x^{∗})$ con $x \neq x^{∗}$ .

Análogamente podemos definir máximo local o global (estricto) para el problema de maximización. Como $x^{∗}$ es un máximo local (global) de (2) si y solo si $x^{∗}$ es un mínimo local (global) del problema

\min - f (x) sujeto a x \in X

(3)

es suficiente estudiar los problemas de minimización.

Para funciones con $n = 1$ o $n = 2$ variables es posible encontrar el área del mínimo local o global a través de una representación geométrica. Para funciones con $n > 2$ variables esto no es posible.

De forma general el problema de minimización se escribe:

\min f (x) sujeto a h (x) = 0, g (x) \leq 0

(4)

donde $h : ℝ^{n} \to ℝ^{p}$ y $g : ℝ^{n} \to ℝ^{m}$ son funciones dadas y la restricción $g (x) \leq 0$ viene dada componente a componente. En este caso, el conjunto factible del problema de optimización (4) viene dado por:

X : = {x \in ℝ^{n} | h (x) = 0, g (x) \leq 0}

(5)

Los problemas de minimización (1) o (2) representan modelos matemáticos de aplicación en el mundo real. Los componentes del vector $x \in R^{n}$ son los parámetros del modelo, los cuales proveen ciertos grados de libertad y se eligen de manera óptima de forma que el modelo tenga las propiedades deseadas.

Los problemas de optimización se pueden clasificar de distinta forma con el objetivo de encontrar un método adecuado para su resolución:

Según su interés particular:

(a) Optimización lineal: f, g y h son funciones afines, esto es:

$\min c^{T} x sujeto a Ax = b, x \geq 0$ (6)

con $A \in ℝ^{pxn}, c \in ℝ^{n}, b \in R^{p}$ .

(b) Optimización cuadrática: f es una función cuadrática y g,h son funciones lineales.

(c) Optimización con restricciones lineales: f es una función no linear pero g y h son lineales.

(d) Optimización convexa: f,g son funciones convexas y h es linear.

(e) Optimización no linear: f, g y h son funciones no lineares
Según la disponibilidad numérica de las derivadas de f, g y h.
Según la derivabilidad de las funciones f, g y h.
Según la dimensión del problema.

Problema de la p-mediana

El problema de la p-mediana es un modelo básico en la teoría de localización discreta y está clasificado como NP-difícil. Se trata de un problema de optimización lineal entera cuyo objetivo es localizar p instalaciones de manera que se minimice la suma de las distancias ponderadas entre los vértices con demanda y las instalaciones seleccionadas.

Definición 4.6. Se llama grafo finito no dirigido a la tupla $G = (V, A, f, p, w)$ donde $V$ es un conjunto no vacío cuyos elementos se denominan vértices, $A$ es un conjunto cuyos elementos se denominan aristas, $f : A \to S^{2} V$ es una aplicación de $A$ en el conjunto $S^{2} V$ de parejas no ordenadas de vértices, $p : A \to ℝ^{+}$ y $w : V \to ℝ^{+}$ son funciones que asignan a cada arista y vértice respectivamente un número real no negativo que llamaremos peso. El peso $p_{i}$ asociado a la arista $a_{i}$ de $G$ representa la longitud del eje; el peso $w_{i}$ asociado al vértice $v_{i}$ de $G$ representa la demanda que hay en ese vértice.

Definición 4.7. La distancia de cualesquiera dos puntos $x$ e $y$ de $G$ se representa por $d (x, y)$ y se define como la longitud del camino más corto en $G$ entre $x$ e $y$ , donde la longitud del camino es la suma de los pesos de las aristas que lo forman.

Definición 4.8. La matriz de distancia $D = (d_{ij})$ en el grafo $G$ se define como:

d_{ij} = {\begin{matrix} d (v_{i}, v_{j}) para i, j = 1, 2, . . ., n con i \neq j \\ 0 en otro caso \end{matrix}

(7)

Definición 4.9. Un punto $x_{0} \in G$ es una mediana absoluta de $G$ si para cada punto $x \in G$ se tiene que:

\sum_{i = 1}^{n} w_{i} d (v_{i}, x_{0}) \leq \sum_{i = 1}^{n} w_{i} d (v_{i}, x)

(8)

Teorema 4.1. Una mediana absoluta de un grafo siempre está en un vértice del mismo.

Se puede expresar el problema de la p-mediana como el problema de optimización:

\begin{equation} \operatorname{min} f(S)=\sum_{i=1}^{n}w_{i}d(v_{i},x_{0})~ sujeto~ a~|S|=p, S\subset G \end{equation}

donde $d (v_{i}, S) : = \min {d (v_{i}, s) | s \in S}$ es la distancia entre cada vértice $v_{i}$ y $S$ .

El matemático iraní-estadounidense Hakimi demostró que la localización óptima de una instalación siempre se encuentra en un vértice del grafo. Según este problema, cada instalación debe estar localizada de manera que la suma de las distancias ponderadas a los vértices que es mínima. Entonces, por el Teorema 3.1 se puede encontrar una configuración óptima de tal manera que cada instalación se localice en un vértice del grafo. Esta propiedad permite expresar el problema de la p-mediana como un problema de optimización lineal entera:

\begin{align} min f (Y, X) = & \sum_{i = 1}^{n} \sum_{j = 1}^{n} w_{i} d_{ij} x_{ij} & (10) \\ sujeto a & \sum_{j = 1}^{n} x_{ij} = 1, i = 1, . . ., n & (11) \\ \sum_{j = 1}^{n} y_{ij} = p & (12) \\ 0 \leq x_{ij} & \leq y_{j}, i, j = 1, . . ., n & (13) \\ y_{ij} & \in {0, 1}, j = 1, . . ., n & (14) \end{align}

donde:

$d_{ij}$ es la distancia entre los vértices $v_{i}$ y $v_{j}$ .
$x_{ij}$ es la demanda que surge en el vértice $v_{i}$ satisfecha por $v_{j}$ (si existe).
$X$ es la matriz formada por las variables $x_{ij}$ .
$y_{j}$ es la variable binaria que decide si un vértice pertenece o no a la p-mediana.
$Y$ denota al vector de las variables $y_{j}$ .

La restricción (11) significa que la demanda en el vértice $v_{i}$ debe ser satisfecha por alguna instalación. La restricción (12) asegura que p vértices pertenezcan a la p-mediana. La restricción (13) evita la asignación de demanda a un vértice que no se encuentre en la p-mediana y garantiza la no negatividad de la demanda. La restricción (14) obliga a $y_{j}$ a ser una variable binaria.

Recopilación y tratamiento de los datos

Se han utilizado dos conjuntos de datos, procedentes del portal de datos abiertos y del portal de Salud de de la Junta de Castilla y León:

Dependencia entre consultorios y centros de salud [Descargado el 27 de septiembre de 2022]
Actividad de Medicina de Familia a nivel de Consultorio [Descargado el 10 de septiembre de 2022]

Del primer conjunto de datos hemos obtenido las direcciones de los consultorios (no hemos tenido en cuenta los Centros de Salud), la zona básica a la que están adscritos y la provincia a la que pertenecen; mientras que del segundo conjunto hemos obtenido una media de los pacientes atendidos cada día en cada consultorio y el tipo de consulta que ha sido (presencial, no presencial o a domicilio).

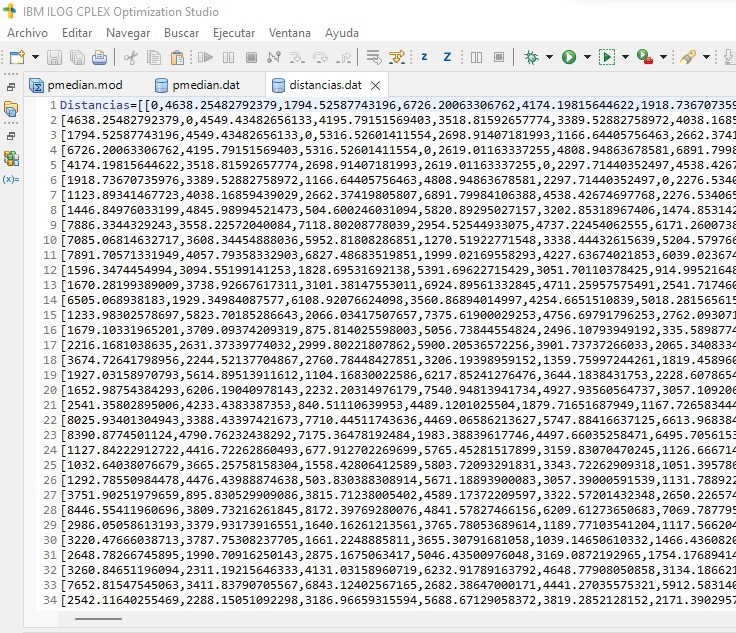
Tras la recopilación de los datos, se han geolocalizado los consultorios médicos a través de Google Earth Pro. Tras esto, se ha realizado el filtrado de datos correspondientes a la provincia de Salamanca y se ha calculado en un Jupyter Notebook la matriz de distancias. Para ello, se han convertido las coordenadas geográficas a radianes. Se ha exportado la matriz en formato .csv y, a través de R-Studio, se ha conseguido el archivo .txt final necesario para el modelo.

Para el cálculo de las distancias se ha utilizado la métrica Haversine, ya que emplea vectores bidimensionales (considerando así la curvatura de la Tierra). En el Apartado Mejoras del modelo indicaremos otras distancias que se pueden utilizar para hacer más realista el modelo. La métrica Haversine mide la distancia en ``línea recta'' sobre la superficie de la tierra

D (x, y) = 2 \arcsin (\sqrt{\sin^{2} (\frac{x_{1} - y_{1}}{2}) + \cos x_{1} \cos y_{1} \sin^{2} (\frac{x_{2} - y_{2}}{2})})

(15)

La elección de los consultorios médicos de la provincia de Salamanca se ha realizado con el fin de mejorar la comprensión del problema, facilitar el manejo de los datos y poner de manifiesto la distribución de estos dentro del sistema sanitario de Castilla y León. Este sistema está dividido en gerencias de salud, que cuentan con autonomía propia y, dentro de este, la gerencia de Salamanca agrupa a todos los consultorios de la provincia.

Descripción del modelo

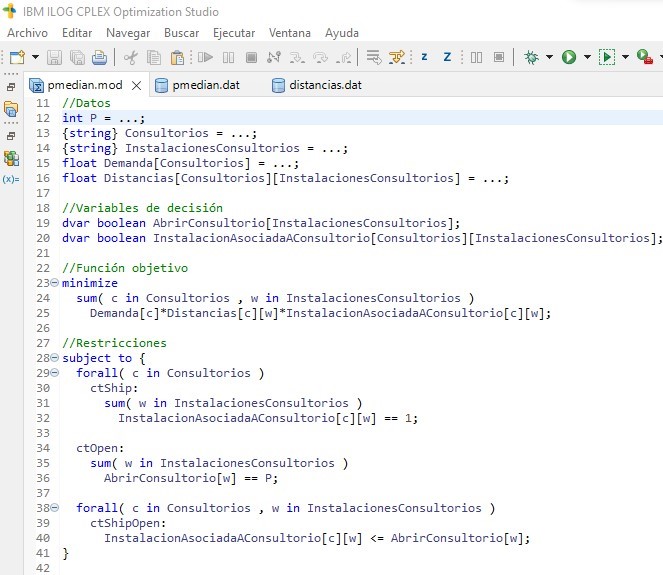
Para la realización del modelo se ha utilizado el paquete de software de optimización IBM ILOG CPLEX Optimization Studio, en su versión 22.1.0.0. El modelo desarrollado pmedian.mod puede verse en la Figura 1 y trata de localizar un número p de consultorios médicos de manera que la distancia entre los núcleos de demanda (consultorios actuales) ponderados con la demanda (número de consultas presenciales actuales) sea mínima. En otras palabras, el modelo abre un consultorio de forma que esté a la menor distancia con respecto al resto de consultorios que le asocia, teniendo en cuenta las consultas que tendrá que atender presencialmente en base a las consultas actuales. De esta forma se consigue reducir los consultorios evitando que los pacientes tengan que recorrer mucha distancia para ser atendidos presencialmente.

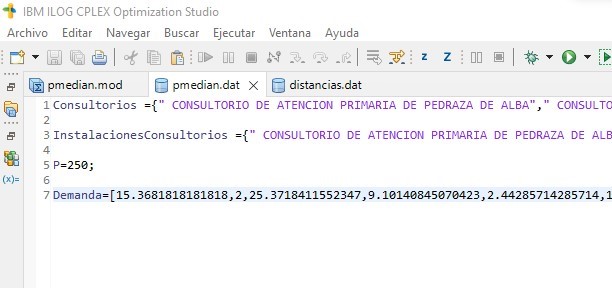
Asimismo, se han creado los ficheros de datos distancias.dat (Figura 3) y pmedian.dat (Figura 2), que contienen la información relativa a la matriz de distancias, consultorios médicos, la demanda de cada consultorio y el número de instalaciones p que se desea localizar.

En nuestro caso, los vértices del grafo utilizado y las posibles instalaciones son los consultorios médicos; la demanda utilizada es el número de consultas presenciales en cada consultorio. El número de instalaciones que se desea localizar varía con cada ejecución del modelo y es lo que llamamos p.

Modelo de la p-mediana en CPLEX. Este modelo ha sido extraído de los ejemplos del programa IBM ILOG CPLEX Optimization Studio — Figura 1: Modelo de la p-mediana en CPLEX. Este modelo ha sido extraído de los ejemplos del programa **IBM ILOG CPLEX Optimization Studio**

Fichero de datos pmedian.dat — Figura 2: Fichero de datos *pmedian.dat*.

Fichero de datos distancias.dat — Figura 3: Fichero de datos *distancias.dat*.

Resultados

Se han realizado diversas ejecuciones del modelo para diferentes valores de p. Tenemos datos de ubicación y consultas de 283 consultorios de la provincia de Salamanca, que son los que hemos utilizado para realizar el modelo. El tiempo de ejecución aproximado ha sido de 2 minutos y 30 segundos, sin diferencias significativas para los distintos valores de p.

p=3: Este caso supone una reducción drástica del número de consultorios. Los consultorios proporcionados por el modelo son los consultorios de las localidades de: Fuenteliante, Machacón y Cristóbal. Se puede ver la distribución en el mapa. Se puede descargar aquí. Como se puede observar, los consultorios obtenidos se sitúan repartidos a lo largo de toda la provincia. Esto era de esperar pues nuestro modelo busca ofrecer una cobertura a todos los consultorios actuales minimizando la distancia que tienen que recorrer los pacientes.
p=141: Se trata de una reducción del 50% de los consultorios. El listado de los 141 consultorios abiertos se pueden consultar en el mapa. Se puede descargar aquí.
p=250: Implica la reducción de 41 consultorios médicos (seleccionamos aproximadamente el 86% de los consultorios actuales). El listado de los 250 consultorios abiertos se puede consultar en el mapa. Se puede descargar aquí.

Mejoras del modelo

Para la realización de este modelo hemos utilizado los datos disponibles en las bases de datos del portal de Datos Abiertos de la Junta de Castilla y León y de SACYL tras un proceso de depuración.

Este modelo se podría mejorar considerando otros datos para los parámetros:

Distancia: Hemos considerado una distancia en ``línea recta'' sobre la superficie terrestre, sin tener en cuenta la orografía del terreno y las carreteras [3]. Podríamos considerar como distancia el tiempo que se tarda en desplazarse de un consultorio a otro, o distancias del recorrido por las distintas carreteras teniendo en cuenta el trazado de estas y el tipo de vía.
Demanda: Hemos considerado como demanda el número de consultas presenciales, pues son las que requieren el desplazamiento de los pacientes al consultorio, pero podríamos haber tenido en cuenta el número de cartillas asociadas a cada consultorio [10], este mismo dato ponderado por la edad de los pacientes (en general no todos los grupos de edad acuden al médico con la misma frecuencia) [7], o la presión asistencial [8].
Consultorios candidatos: Hemos tenido en cuenta todos los consultorios de Salamanca sin considerar los centros de salud. Para este modelo podríamos haber reducido el número de candidatos a nuevos consultorios tras un análisis de aquellos que tienen mejores instalaciones y mejores recursos, o aquellos que cuenten con una farmacia en la misma localidad. [8]
Modelo: Hemos utilizado el modelo de la p-mediana. También se podría realizar la modelización de otros problemas como el problema del p-centro, que minimiza las distancias entre las instalaciones y el nodo de demanda situado a mayor distancia, o el problema de máxima cobertura, que maximiza la cobertura sobre la demanda de una población con recursos limitados.

Conclusiones

Tras aplicar el modelo la p-mediana a nuestro problema hemos obtenido una distribución de consultorios que optimiza la distancia que tienen que recorrer los pacientes para ser atendidos y supone una reducción de costes al disminuir el número de instalaciones, con lo que se puede invertir este dinero en mejorar los consultorios que seguirían prestando servicios. Asimismo, el modelo nos proporciona el consultorio al que quedarían adscritos aquellos consultorios que, según el modelo, no se abrirían. Este resultado no lo hemos tenido en cuenta ya que los consultorios están adscritos a un centro de salud y estos no los hemos considerado en el estudio. Cabe destacar con esto la importancia del modelo, el cual se podría utilizar, por ejemplo, para estudiar si los centros de salud y sus respectivos consultorios médicos asociados están bien distribuidos con respecto al modelo estudiado. Además solucionaríamos el problema de la falta de profesionales sanitarios en la Atención Primaria.

Esta propuesta no busca que la calidad de los servicios de salud en las localidades que no tengan consultorio empeore, sino que sugerimos que los pacientes sean visitados por un vehículo medicalizado con una dotación de material y personal adecuada. De esta forma la atención podría ser mejor ya que en algunos consultorios ahora mismo no se atiende a los pacientes presencialmente todos los días. Además, el aumento de las consultas no presenciales tras la pandemia de Covid-19 favorece la implantación de este modelo, puesto que muchas gestiones se pueden realizar de forma telemática.

Un adecuado tratamiento de los datos favorece la toma de decisiones y la modelización de estos a través de modelos matemáticos facilita este proceso. Aun así, es indispensable contar con el trabajo de personal sanitario, gerentes, ingenieros, matemáticos y políticos, expertos cada uno en su campo y conscientes de los problemas específicos, para elaborar un modelo que permita obtener una solución adecuada al problema de la Atención Primaria de Castilla y León. El trabajo en equipo e interdisciplinar es imprescindible en la elección de datos y parámetros correctos. El número de consultorios a establecer se ha de determinar con un estudio más exhaustivo del personal disponible, las características sociales y geográficas de la comunidad, y el material y las instalaciones existentes.

Este trabajo pone de manifiesto la utilidad de las matemáticas en problemas reales y destaca el valor económico y social de los datos abiertos.

Bibliografía

[1] El Norte de Castilla, La zona de Saldaña perderá cuatro de los doce médicos de plantilla, https:/www.elnortedecastilla.es/palencia/zona-saldana-perdera-20220922234139-nt.html, sep 2022, [Visitado el 3 de octubre de 2022].

[2] El Mundo. Diario de Castilla y León, El déficit de médicos de familia alcanza las 314 plazas sin cubrir en Castilla y León, https:/diariodecastillayleon.elmundo.es/articulo/castilla-y-leon/deficit-medicos-familia-alcanza-314-plazas-cubrir-castilla-leon/20211212192659037816.html, dec 2021, [Visitado el 18 de septiembre de 2022].

[3] Junta de Castilla y León, Catálogo de la red regional de carreteras (tramificada)., https:/analisis.datosabiertos.jcyl.es/explore/dataset/catalogo-de-la-red-regional-de-carreteras-tramificada/table/, sep 2022, [Visitado el 30 de septiembre de 2022].

[4] IBM, Documentación de IBM ILOG CPLEX Optimization Studio V22.1.0, https://www.ibm.com/docs/es/icos/22.1.0?topic=SSSA5P_22.1.0/ilog.odms.studio.help/Optimization_Studio/topics/COS_home.html, sep 2022, [Visitado el 27 de septiembre de 2022].

[5] IBM, Modelo p-mediana, https:/www.ibm.com/docs/es/icos/20.1.0?topic=SSSA5P_20.1.0/ilog.odms.ide.help/examples/html/opl/pmedian/pmedian.mod.html, sep 2022, [Visitado el 27 de septiembre de 2022].

[6] Sofía Led Jiménez, Problemas de la p-mediana. Aplicación, Trabajo de fin de grado en matemáticas, Universidad de Zaragoza, jul 2018.

[7] Junta de Castilla y León, Ciudadanos con derecho a la asistencia sanitaria., https:/datosabiertos.jcyl.es/web/jcyl/set/es/salud/poblacion-referencia/1285114749493, sep 2022, [Visitado el 30 de septiembre de 2022].

[8] Junta de Castilla y León, Pacientes diarios en consulta ordinaria., https:/analisis.datosabiertos.jcyl.es/explore/dataset/presion-asistencial-mf-pediatria-y-enfermeria-zbs/table/, sep 2022, [Visitado el 30 de septiembre de 2022].

[9] Junta de Castilla y León, Registro de establecimientos farmacéuticos de Castilla y León., https://analisis.datosabiertos.jcyl.es/explore/dataset/registro-de-establecimientos-farmaceuticos-de-castilla-y-leon/table/?disjunctive.nombre_comercial&disjunctive.localidad&disjunctive.municipio, sep 2022, [Visitado el 30 de septiembre de 2022].

[10] Junta de Castilla y León, Tarjetas sanitarias por profesional y zona básica de salud., https:/analisis.datosabiertos.jcyl.es/explore/dataset/tsi-por-profesional/table/, sep 2022, [Visitado el 30 de septiembre de 2022].

[11] Bryan Salazar López, ¿Cómo calcular una matriz de distancias para modelar un VRP?, https://www.ingenieriaindustrialonline.com/investigacion-de-operaciones/como-calcular-una-matriz-de-distancias-para-modelar-un-vrp/, sep 2022, [Visitado el 21 de septiembre de 2022].

[12] Consumo y Bienestar Social Ministerio de Sanidad, Indicadores clave del Sistema Nacional de Salud, http:/inclasns.msssi.es/main.html?permalink=91ecb5290f0b60173bf7b6faaf35cc96, sep 2022, [Visitado el 18 de septiembre de 2022].

[13] SACYL, Guía de ordenación sanitaria de Castilla y León en el Área de Salud de Salamanca, https:/www.saludcastillayleon.es/institucion/es/organizacion/ordenacion-sistema-sanitario/guia-ordenacion-sanitaria-castilla-leon/area-salud-salamanca.ficheros/77569-Salamanca.pdf, sep 2022, [Visitado el 27 de septiembre de 2022].

[14] SACYL, Informes estadísticos de los Recursos Sanitarios Públicos. Ficheros por año., https:/www.saludcastillayleon.es/transparencia/es/transparencia/sanidad-cifras/informes-estadisticos/ordenacion-alfabetica/recursos-sanitarios-publicos, sep 2022, [Visitado el 18 de septiembre de 2022].

Aplicación del problema de la p-mediana a la Atención Primaria en Castilla y León

Ernesto Ramos Pérez

Carlos Montero Pascual